Bir Motosiklet Ne Kadar Yatırılabilir?

Yazar: Ahmet TEZCAN

Özellikle MotoGP yarışlarında korkunç şekilde yatırılan motosikletleri görünce çoğumuz bu duruma şaşırıyoruz. Yüksek hızlarda motosikletlerin bu denli yatırılması nasıl mümkün oluyor? Yatırma açısının hesabı ve detaylar için okumaya devam edin…

Özellikle MotoGP yarışlarında pilotların viraj alırken motosikletleri ne kadar yatırdığını görünce bunun sanki bir sihir olduğunu düşünürüz. Bu yazımızda, motosikleti yatırmanın bir sihir olmadığını, aksine tamamen bilime dayandığı için hesaplanabileceğine değineceğiz.

Açıyı Hesaplamak

Yatırma açısını hesaplamak için bir kuvvet diyagramı ile başlanır. İlk olarak unutulmaması gereken şey, bu hesaplamada yer çekimi merkezinin sahte kuvvet merkezi (sahte kuvvet hareketlerinin öngörülebileceği konum) ile aynı konumda olduğu varsayılıyor.

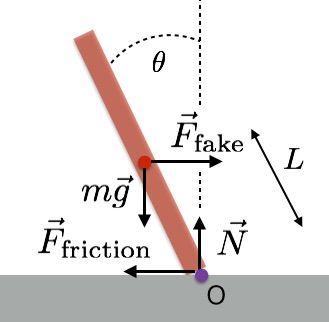
Eğer sahte kuvvet bir hızlanma referans çerçevesinde kullanılıyorsa, net kuvvet sıfıra eşit olur. Bu, hem X hem de Y yönlerinde net kuvvet olarak yazılabilir.

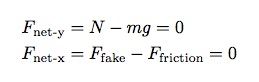
Sahte kuvvet, kütle çarpı ivmenin negatif değeridir. Bu da net kuvvet için aşağıdaki iki denklemi verir.

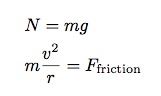
Şimdi toplam tork, O noktası civarına yazılabilir. Sürtünme kuvveti ve normal kuvvet, O noktasından geçene kadar sıfır torka sahiptir.

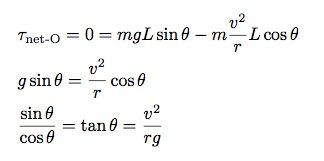
Bu da demek oluyor ki viraja daha hızlı girildiğinde motosikletin daha çok yatırılması gerekiyor. Daha dar virajlarda (daha küçük yarı çap yani “r”) daha çok yatırma gerekiyor fakat bunun sınırı ne? Bu sınır sürtünme kuvvetine bağlı. Eğer maksimum sürtünme kuvveti hesaplanırsa, bu hesaplamanın sonucu, maksimum yatırma açısını hesaplamak için kullanılabilir. Statik sürtünme kuvvetinin olağan modeli (kaymayan bir lastik için), bu sürtünme kuvvetinin normal kuvvet ile orantılı olduğunu gösteriyor.

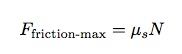
Tabii ki normal kuvvet için de bir ifade mevcut. Hepsini bir araya getirdiğimizde ortaya bu çıkıyor:

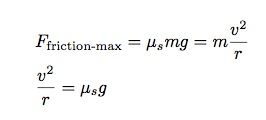
Bu, yatırma açısı hesaplaması ile birleştiriliyor:

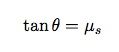
Peki statik sürtünmenin (μs) katsayısı ne olabilirdi? Eğer katsayı 0.7 olarak ele alınırsa, yatırma açısı 35 derece olarak çıkıyor. Ancak, yarış motosikletleri 60 dereceden fazla bir açıda yatırılabiliyor. Ters yönde çalışarak bu büyük yatırma açısı için sürtünme katsayısı çözülüyor ve 1.7 değeri çıkıyor.

Sürtünme katsayısı 0 ve 1 arasında olduğu düşünülürken nasıl oluyor da 1.7 değeri bulunuyor? Bunu cevabı: sürtünme mevzuu gerçekten karmaşık. Sürtünme kuvvetinin tipik modeli, μ’nun 1’den az olduğunu söylüyor fakat böyle olmak zorunda olduğu söylenmiyor.

Motosikletlerin Sürtünme Katsayıları Var Mıdır?

Viraj alan bir motosiklete bakıp ivmesi tahmin edilebilir mi? Bu ivmeden, tahmini bir sürtünme katsayısı elde edilebilir.

İşte viraj alan bir motosiklet üstten görünümü:

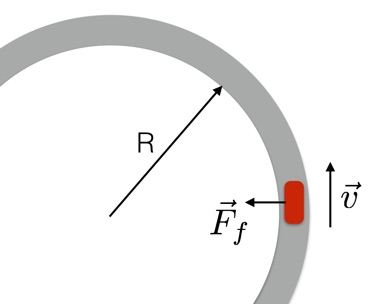
Sürtünme için basit model, bir daire içinde hareket eden bir nesnenin ivmesinin ifadesi ile birlikte varsayılırsa ortaya bu çıkıyor:

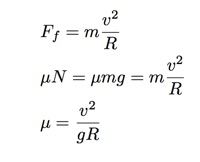
Şimdi bir MotoGP pistine bakıp farklı virajlarda motosiklet hızlarını bularak sürtünme katsayısı hesaplamasına değinelim. Hesaplamalar için Jerez pistine ait özel hız haritası kullanılarak aşağıdaki iki viraj ele alınır.

Viraj 4: Yarı Çap= 114.8 m, Hız = 35.6 m/s, a = 10.98 m/s2, μmin = 1.12Viraj 5: Yarı Çap = 35.34 m, Hız= 20.9 m/s, a = 12.41 m/s2, μmin = 1.27

Bunlar sadece iki viraj. Yarı çap tahminlerine göre, bir motosikletin kaymadan viraj alabilmesi için ikisinin de 1’den daha büyük bir sürtünme katsayısına ihtiyacı var. Bu yüzden, 1.7’lik bir sürtünme katsayısı çılgınca yüksek görünebilir fakat gösterildiği gibi katsayının 1’den büyük olması mümkün.